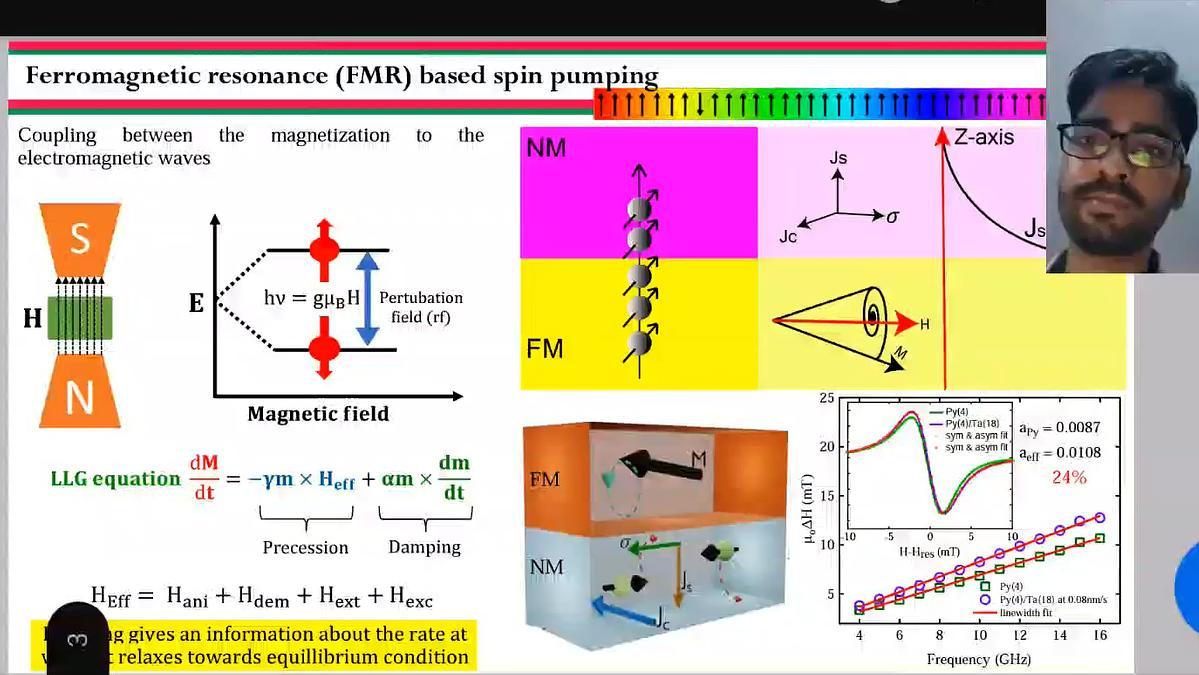
Spin-orbit coupling (SOC) plays a vital role in spin-to-charge interconversion in heavy metal (HM)-ferromagnet (FM) bilayer structures 1. Spin pumping is an efficient method to generate pure spin current by the precessional motion of magnetization, which transfers angular momentum to HM. The efficiency of spin pumping is quantified by an interfacial parameter called spin-mixing conductance (g↓↑). Electrical detection of spin current is possible via inverse spin Hall effect (ISHE) which converts spin current into charge current. The efficiency of spin-to-charge interconversion is quantified by spin Hall angle (θSH) 2. The θSH of heavy metal highly depends on its crystalline phase and the effect of the seed layer on the phase of HMs is largely overlooked. Here, we report the effect of seed permalloy (Ni80Fe20, Py) layer thickness on the Tantalum (Ta) and Tungsten (W) crystalline phase and its θSH. We have observed a structural phase transition in Ta as a function of seed layer thickness (tPy) affecting the θSH of the Ta layer. Due to strain at the interface between crystalline Py and Ta, Ta exhibits a mixed-phase (α+β) on the seed permalloy layer when tPy > 12 nm. However, Ta nucleates as α-Ta on Py with tPy < 8 nm, Py does not exhibit prominent crystalline nature. The phase transition of Ta is primarily attributed to strain at the Py/Ta interface which is not observed in both Py(tPy)/W(10) and Co40Fe40B20 (tCFB)/Ta(18) bilayer structure. Ferromagnetic resonance (FMR) based spin pumping shows that effective damping is enhanced for all samples. The maximum g↓↑ of 10.1×1018 m-2 is observed for Si/Py(20)/Ta(18) and the minimum value of 7.9×1018 m-2 for Si/Py(8)/Ta(18) which corresponds to (α+β)-phase of Ta and α-phase of Ta, respectively. The estimated θSH for (α+β)-Ta is 0.15 ± 0.009, which is higher than α-Ta. The combined effect of symmetry breaking and low longitudinal resistance are the primary reason for the high g↓↑ and θSH. Our systematic study provides an insight into Ta phase transition via seed layer thickness and gives an alternative route for tuning 3.

References*
1 A. Brataas, Y. V. Nazarov, and G. E. W. Bauer, Finite-Element Theory of Transport in Ferromagnet–Normal Metal Systems, Phys. Rev. Lett. 84, 2481 (2000). 2 Y. Tserkovnyak, A. Brataas, and G. E. W. Bauer, Nonlocal Magnetization Dynamics in Ferromagnetic Heterostructures, Rev. Mod. Phys. 77, 1375 (2005). 3 K. Sriram, A. Haldar, and C. Murapaka, Effect of Seed Layer Thickness on the Ta Crystalline Phase and Spin Hall Angle, Nanoscale 13, 19985 (2021).